Inverse kinematics

An example of how tlm can be used to solve a simple 3D inverse kinematics problem.

python

import torch
import torch.nn as nn
import torchlensmaker as tlm

y1 = tlm.parameter(torch.tensor(-20))
z1 = tlm.parameter(torch.tensor(0))

y2 = tlm.parameter(torch.tensor(0))
z2 = tlm.parameter(torch.tensor(0))

length1 = tlm.parameter(10.)

class Target(tlm.SequentialElement):
    def __init__(self, point):
        super().__init__()
        self.point = point

    def forward(self, inputs):
        return inputs.replace(loss=torch.linalg.vector_norm(inputs.target() - self.point))

model = tlm.Sequential(
    tlm.Gap(length1),
    tlm.Rotate3D(y1, z1),
    tlm.Gap(5),
    tlm.Rotate3D(y2, z2),
    tlm.Gap(5),
    Target(torch.Tensor([20, 6, 6])),
)

for name, param in model.named_parameters():
    print(name, param)

tlm.show3d(model)

0.offset Parameter containing:
tensor(10., dtype=torch.float64, requires_grad=True)
1.y Parameter containing:
tensor(-20., dtype=torch.float64, requires_grad=True)
1.z Parameter containing:
tensor(0., dtype=torch.float64, requires_grad=True)
3.y Parameter containing:
tensor(0., dtype=torch.float64, requires_grad=True)
3.z Parameter containing:
tensor(0., dtype=torch.float64, requires_grad=True)

python

import torch.optim as optim


tlm.optimize(
    model,
    optimizer = optim.Adam(model.parameters(), lr=0.5),
    sampling = {},
    dim = 3,
    num_iter = 100
).plot()

print("length:", length1.item())
print("y1:", torch.rad2deg(y1).detach().numpy())
print("z1:", torch.rad2deg(z1).detach().numpy())
print("y2:", torch.rad2deg(y2).detach().numpy())
print("z2:", torch.rad2deg(z2).detach().numpy())

tlm.show3d(model)

[  1/100] L= 6.55889 | grad norm= 0.21135987435455386
[  6/100] L= 5.70286 | grad norm= 0.19257733083413983
[ 11/100] L= 4.91661 | grad norm= 0.18926838686398062
[ 16/100] L= 4.17533 | grad norm= 0.18662699239622438
[ 21/100] L= 3.48814 | grad norm= 0.181107064165984
[ 26/100] L= 2.84906 | grad norm= 0.17672399946947678
[ 31/100] L= 2.25372 | grad norm= 0.17132386834441754
[ 36/100] L= 1.69690 | grad norm= 0.1637112214861123
[ 41/100] L= 1.18260 | grad norm= 0.15121938783228422
[ 46/100] L= 0.72997 | grad norm= 0.12873488863008611
[ 51/100] L= 0.36213 | grad norm= 0.10496851849244897
[ 56/100] L= 0.12291 | grad norm= 0.5631310292340369
[ 61/100] L= 0.13402 | grad norm= 0.4735101822994557
[ 66/100] L= 0.24981 | grad norm= 0.7226007852751372
[ 71/100] L= 0.14604 | grad norm= 0.232030575224137
[ 76/100] L= 0.11556 | grad norm= 0.7742936889836994
[ 81/100] L= 0.10944 | grad norm= 1.008243504355836
[ 86/100] L= 0.12821 | grad norm= 0.9000438629914546
[ 91/100] L= 0.07294 | grad norm= 0.7805575308068743
[ 96/100] L= 0.02507 | grad norm= 1.0019158648420319
[100/100] L= 0.15007 | grad norm= 0.9773011050829061

png

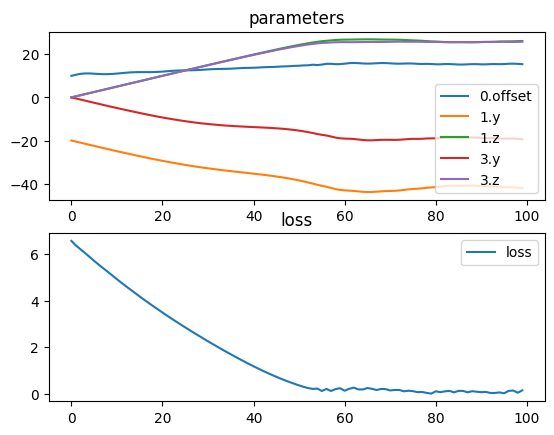
length: 15.370180262268784
y1: -2415.425926644128
z1: 1500.4004010528536
y2: -1114.1854533749918
z2: 1480.6892968482773

Inverse kinematics ​

Inverse kinematics